Perhaps the second most famous law in electronics after Ohm’s law is Moore’s law: the number of transistors that can be made on an integrated circuit doubles every two years or so. Since the physical size of chips remains roughly the same, this implies that the individual transistors become smaller over time. We’ve come to expect new generations of chips with a smaller feature size to come along at a regular pace, but what exactly is the point of making things smaller? And does smaller always mean better?
Smaller Size Means Better Performance
Over the past century, electronic engineering has improved massively. In the 1920s, a state-of-the-art AM radio contained several vacuum tubes, a few enormous inductors, capacitors and resistors, several dozen meters of wire to act as an antenna, and a big bank of batteries to power the whole thing. Today, you can listen to a dozen music streaming services on a device that fits in your pocket and can do a gazillion more things. But miniaturization is not just done for ease of carrying: it is absolutely necessary to achieve the performance we’ve come to expect of our devices today.
One obvious benefit of smaller components is that they allow you to pack more functionality in the same volume. This is especially important for digital circuits: more components means you can do more processing in the same amount of time. For instance, a 64-bit processor can, in theory, process eight times as much information as an 8-bit CPU running at the same clock frequency. But it also needs eight times as many components: registers, adders, buses and so on all become eight times larger. So you’d need either a chip that’s eight times larger, or transistors that are eight times smaller.
The same thing holds for memory chips: make smaller transistors, and you have more storage space in the same volume. The pixels in most of today’s displays are made of thin-film transistors, so here it also makes sense to scale them down and achieve a higher resolution. However, there’s another, crucial reason why smaller transistors are better: their performance increases massively. But why exactly is that?
It’s All About the Parasitics
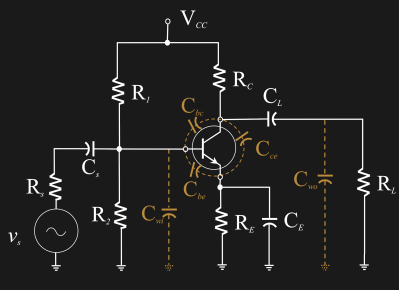
Whenever you make a transistor, it comes with a few additional components for free. There’s resistance in series with each of the terminals. Anything that carries a current also has self-inductance. And finally, there’s capacitance between any two conductors that face each other. All of these effects eat power and slow the transistor down. The parasitic capacitances are especially troublesome: they need to be charged and discharged every time the transistor switches on or off, which takes time and current from the supply.
The capacitance between two conductors is a function of their physical size: smaller dimensions mean smaller capacitances. And because smaller capacitances mean higher speed as well as lower power, smaller transistors can be run at higher clock frequencies and dissipate less heat while doing so.
Capacitance is not the only effect that changes when you scale down a transistor: lots of weird quantum-mechanical effects pop up that are not apparent for larger devices. In general however, making transistors smaller makes them faster. But there’s more to electronics than just transistors. How do other components fare when you scale them down?
Not So Fast
In general, passive components like resistors, capacitors and inductors don’t become much better when you make them smaller: in many ways, they become worse. Miniaturizing these components is therefore done mainly just to be able to squeeze them into a smaller volume, and thereby saving PCB space.
Resistors can be reduced in size without much penalty. The resistance of a piece of material is given by 
| Metric | Imperial | Power rating (W) |
|---|---|---|
| 2012 | 0805 | 0.125 |
| 1608 | 0603 | 0.1 |
| 1005 | 0402 | 0.06 |
| 0603 | 0201 | 0.05 |
| 0402 | 01005 | 0.031 |
| 03015 | 009005 | 0.02 |
Today, the smallest resistors you can buy are metric 03015 size (0.3 mm x 0.15 mm). With a power rating of just 20 mW, they’re only used in circuits that dissipate very little power and are extremely constrained in volume. An even smaller metric 0201 package (0.2 mm x 0.1 mm) has been announced, but is not in production yet. But even when they do show up in manufacturer’s catalogs, don’t expect them to pop up everywhere: most pick-and-place robots are not accurate enough to handle them, so they will likely remain a niche product.
Capacitors can be scaled down as well, but this reduces their capacitance. The formula for calculating the capacitance of a parallel-place capacitor is 
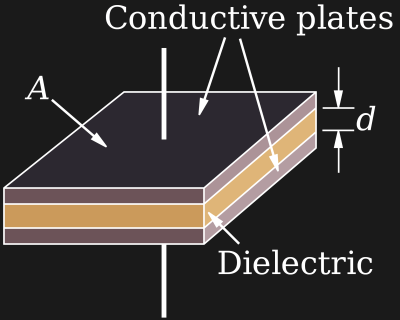
The smallest capacitors available today are packaged in the ultra-small metric 0201 package: just 0.25 mm x 0.125 mm. Their capacitance is limited to a still useful 100 nF with a 6.3 V maximum operating voltage. Again, these packages are so tiny that advanced equipment is needed to process them, limiting their widespread adoption.
For inductors, the story is a bit trickier. The inductance of a straight coil is given by 
The smallest commercially available discrete inductors are in the imperial 01005 size (0.4 mm x 0.2 mm). These go up to 56 nH, with several Ohms of resistance. Inductors in the ultra-small metric 0201 package were announced back in 2014 but apparently never brought to market.
There have been some efforts to get around the inductor’s physical limitations by using a phenomenon called kinetic inductance, which can be observed in coils made of graphene. But even that gives an improvement of perhaps 50%, if it can be made in a commercially viable way. In the end, coils simply don’t miniaturize very well. But this doesn’t have to be a problem if your circuits work at high frequencies. If your signals are in the GHz range, then a coil of a few nH is often enough.
It’s Not Just the Components
This brings us to another thing that has been minaturized over the past century, but which you might not notice right away: the wavelengths we use for communication. Early radio broadcasts used medium wave AM frequencies around 1 MHz, with a wavelength of about 300 meters. The FM band centered around 100 MHz, or three meters, became popular around the 1960s, while today we mostly use 4G communications around 1 or 2 GHz, about 20 cm. Higher frequencies mean more capacity to transmit information, and it’s because of miniaturization that we have cheap, reliable and power efficient radios working at these frequencies.
Shrinking wavelengths enabled shrinking antennas, since their size is directly related to the frequency they need to transmit or receive. The fact that mobile phones today don’t need long protruding antennas is thanks to the fact that they exclusively communicate at GHz frequencies, for which the antennas only need to be around one centimeter long. This is also why most phones that still contain an FM receiver require you to plug in your headphones before using it: the radio needs to use the headphone’s wires as an antenna to get enough signal strength out of those meter-long waves.
As for the circuits connected to our tiny antennas, they actually become easier to make when they’re smaller. This is not just because the transistors become faster, but also because transmission line effects are less of an issue. In a nutshell, when a piece of wire is longer than about one tenth of a wavelength, you need to take the phase shift along its length into account when designing your circuit. At 2.4 GHz this means that just one centimeter of wire already affects your circuit; quite a headache if you’re soldering discrete components together, but not a problem if you’re laying out circuits on a few square millimeters.
How Low Can You Go?
It has become a bit of a recurring theme in tech journalism to either predict the demise of Moore’s law, or to show how those predictions are wrong time and again. The fact remains that the three players still competing at the cutting edge of this game — Intel, Samsung and TSMC — keep on squeezing ever more functionality into each square micron, and are planning several improved generations of chips into the future. Even if the strides they make at each step may not be as great as they were two decades ago, miniaturization of transistors continues nonetheless.
As for discrete components however, it seems like we’ve reached a natural limit: making them smaller doesn’t improve their performance, and the smallest components currently available are smaller than the vast majority of use cases need. There doesn’t seem to be a Moore’s law for discretes, but if there were one, we would love to see how far one could push the SMD Soldering Challenge.
Header image: Jon Sullivan, public domain.
No comments:
Post a Comment